[WIP] Geometrical study about the dome of Sant'Ivo at Sapienza university

[ W I P ]

This is a work in progress post, I am still inserting images and text, I hope it'll be ready soon!

Hi everyone!

This is my first post in this blog, so I would like to introduce myself: my name is Lorenzo Pirone, i'm attending a master degree in Architectural Design in Roma 3 university, Italy.

I started using Grasshopper for Rhino one year ago, and in this first post I will talk about my first experience with this software, that is an ongoing work.

Actually my interest for Grasshopper started thanks to this work, which is about the geometry of the internal surface of the dome of Sant’Ivo at Sapienza University (Rome).

The first time I had to deal with this shape was during an exam in which we had to study the geometric functions hidden in that dome with Wolfram Mathematica.

We begun understanding its shape thanks to a thesis from some students from La Sapienza University. They had a point cloud of the surface, thanks to which they could appreciate its logic: it depends on different geometrical entities and their variation in Z axis is related to a specific curve. The incredible thing is that intersections of the surface with horizontal planes always result in polycurves made of straight segments and circular arcs. This arcs respond to a very strict constrain, as they are defined by the intersection of a set of horizontal planes with vertical lines and planar curves belonging to vertical planes.

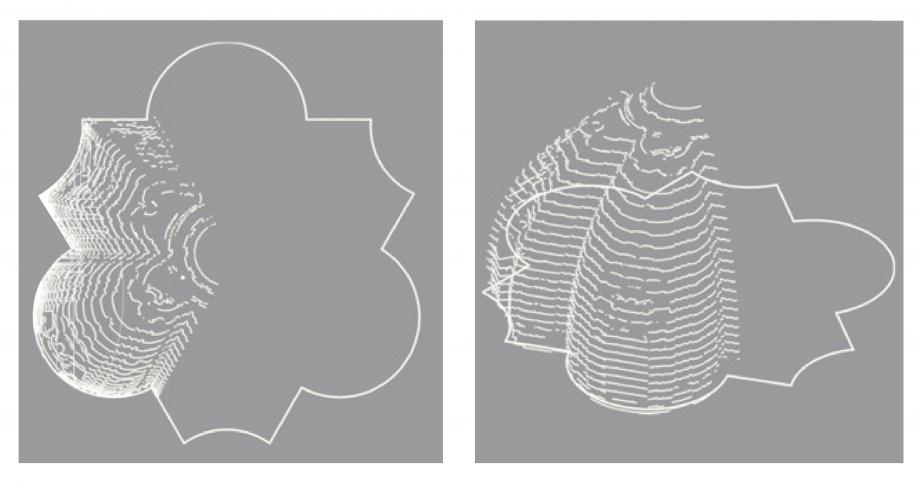
This is the main information we needed to start the geometrical study.

With Wolfram Mathematica it was very difficult to impose this limit. Surfaces were created singularly lofting horizontal curves at different heigts, and the final result was the overlay of the shape modeled in Rhinoceros and the only 2 surfaces from Mathematica.

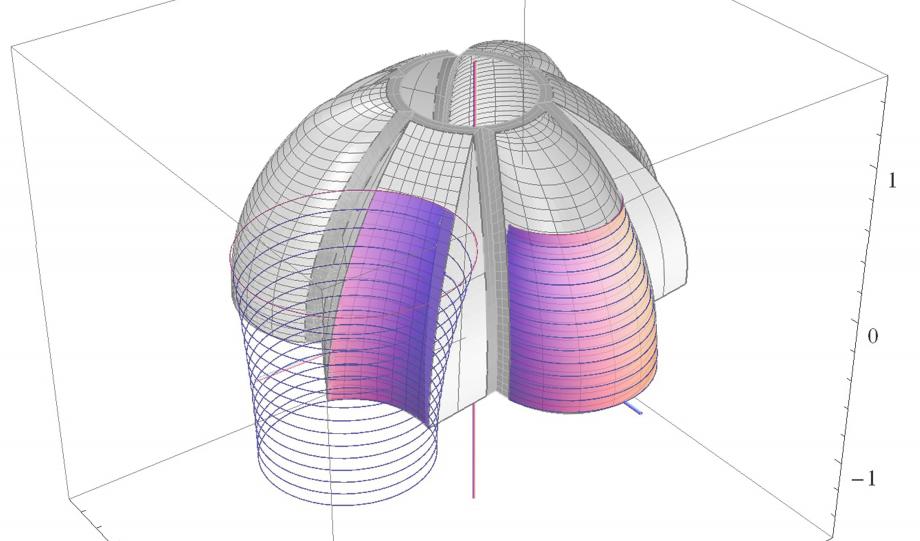
One year after the exam I came across Grasshopper, and I understood immediately  that thanks to its functioning and logics I would have been able to model and control that shape in a more dynamic way.

FIRST GH FILES

At the beginning I knew nothing about the nodes, I kept discovering them day by day. So the first code was pretty complicated and unefficient.

As my experience with GH was growing I periodically updated the file, but the structure of some parts of the code was meant to be changed too, so I restarted it a couple of times, ending up with 13 versions of the code.

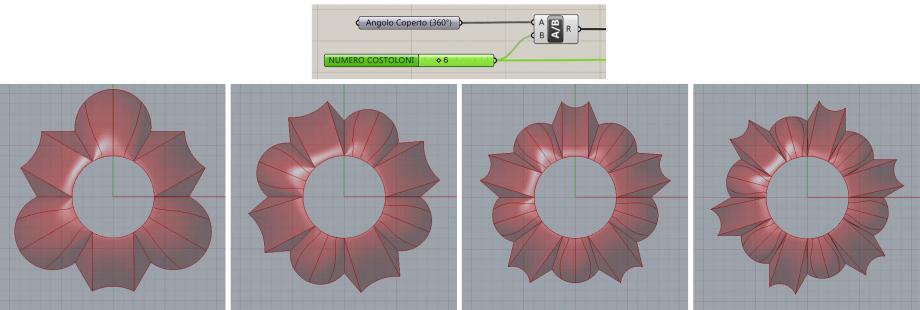
One of the initial challenges was to parametrize the shape completely in order to be able to change the foundamental plan geometry (that is the number of the apses (the concavities) and convexities in the surface). This goal was achieved with one simple constrain: the plan geometry is defined by a closed curve, so its domain is a perigon angle (360°). The 2 different kinds of surfaces of the dome (the apses and the convexities) are alternated covering completely the perigon angle, and every apse or convexity occupies the same angle. In the real configuration there are 6 portions and so each one of them is 60° wide (360°/6). The final geometry is a polar array of the two basic surfaces, that are defined using that angle as a fundamental parameter. If I change the number of portion the angle itself changes, and the geometry with it. This way I can imagine alternative versions of  the dome, in which there is a square or an hexagon as  the fundamental geometric construction instead of the original triangle.

Completing this part of the code was very interesting but it was not the main goal. As we did in Mathematica I wanted to overlay the Grasshopper geometry to the “real” one, trying to get as closer as I could in order to approximate it. This can be done using the correct geometries and tuning the parameters properly.

But in the first experience the “real geometry” was just a 3D surface modeled by ourselves. This time I was looking for something more accurate, so I managed to get my own pointcloud from photos of the dome itself, using PhotoScan.

The output was an obj file, that I could not read with Rhinoceros (still don’t know why). So I exported the coordinates in txt. My intent was making Grasshopper read that text file, but the coordinates of the approximately 64k points could not be red properly because they were written in this form:

X1 Y1 Z1 R1 G1 B1;

[…]

Xn Yn Zn Rn Gn Bn.

I needed to insert line breaks after each value, erase the punctuation and ignore the color information, because as far as I know it is not possible to assign colors to points in Grasshopper.

The line breaks insertion and the punctuation deleting were achieved using a simple text editing software such as Word.

X1

Y1

Z1

R1

G1

B1

The selection of the data was entrusted to Grasshopper itself.

X1

Y1

Z1

(R1)

(G1)

(B1)